Alunos do 2º A e 2º C...segue o vídeo conforme combinado...
Blog do Prof Mauro Ricardo
sábado, 19 de setembro de 2015
sábado, 20 de junho de 2015
sexta-feira, 19 de junho de 2015
REGRA DE CRAMER
REGRA DE CRAMER
A regra de Cramer é uma das maneiras de resolver um sistema linear, mas só poderá ser utilizada na resolução de sistemas que o número de equações e o número de incógnitas forem iguais.
Portanto, ao resolvermos um sistema linear de n equações e n incógnitas para a sua resolução devemos calcular o determinante (D) da equação incompleta do sistema e depois substituirmos os termos independentes em cada coluna e calcular os seus respectivos determinantes e assim aplicar a regra de Cramer que diz:
Os valores das incógnitas são calculados da seguinte forma:
x1 = D1
D
x2 = D2
D
x3 = D3 ... xn = Dn
D D
Veja no exemplo abaixo de como aplicar essa regra de Cramer:
Dado o sistema linear
Devemos encontrar a matriz incompleta desse sistema linear que será chamada de A.
Agora calculamos o seu determinante que será representado por D.
D = 1 + 6 + 2 + 3 – 1 + 4
D = 15.
Agora devemos substituir os temos independentes na primeira coluna da matriz A, formando assim uma segunda matriz que será representada por Ax.
Agora calcularmos o seu determinante representado por Dx.
Dx = 8 + 4 + 3 + 2 – 8 + 6
Dx = 15
Substituímos os termos independentes na segunda coluna da matriz incompleta formando a matriz Ay.
Agora calcularmos o seu determinante Dy.
Dy = -3 + 24 + 4 – 9 – 2 + 16
Dy = 30
Substituindo os termos independentes do sistema na terceira coluna da matriz incompleta formaremos a matriz Az.
Agora calculamos o seu determinante representado por Dz.
Dz = – 2 + 18 + 16 + 24 – 3 – 8
Dz = 45
Dz = 45
Depois de ter substituído todas as colunas da matriz incompleta pelos termos independentes, iremos colocar em prática a regra de Cramer.
A incógnita x = Dx = 15 = 1
D 15
A incógnita y = Dy = 30 = 2
D 15
A incógnita z = Dz = 45 = 3
D 15
Portanto, o conjunto verdade desse sistema será V = {(1,2,3)}.
A incógnita x = Dx = 15 = 1
D 15
A incógnita y = Dy = 30 = 2
D 15
A incógnita z = Dz = 45 = 3
D 15
Portanto, o conjunto verdade desse sistema será V = {(1,2,3)}.
Bom final de semana...
Prof Mauro Ricardo
quinta-feira, 18 de junho de 2015
Determinantes
Determinantes
Como já vimos, matriz quadrada é a que tem o mesmo número de linhas e de colunas (ou seja, é do tipo nxn).
A toda matriz quadrada está associado um número ao qual damos o nome de determinante.
Dentre as várias aplicações dos determinantes na Matemática, temos:
- resolução de alguns tipos de sistemas de equações lineares;
- cálculo da área de um triângulo situado no plano cartesiano, quando são conhecidas as coordenadas dos seus vértices;
Determinante de 1ª ordem
Dada uma matriz quadrada de 1ª ordem M=[a11], o seu determinante é o número real a11:
det M =Ia11I = a11
Observação: Representamos o determinante de uma matriz entre duas barras verticais, que não têm o significado de módulo.
Por exemplo:
|
|
Determinante de 2ª ordem
Dada a matriz  , de ordem 2, por definição o determinante associado a M, determinante de 2ª ordem, é dado por:
, de ordem 2, por definição o determinante associado a M, determinante de 2ª ordem, é dado por:
 , de ordem 2, por definição o determinante associado a M, determinante de 2ª ordem, é dado por:
, de ordem 2, por definição o determinante associado a M, determinante de 2ª ordem, é dado por: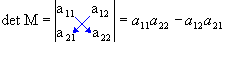
Portanto, o determinante de uma matriz de ordem 2 é dado pela diferença entre o produto dos elementos da diagonal principal e o produto dos elementos da diagonal secundária. Veja o exemplo a seguir.
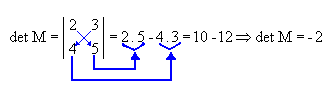
Menor complementar
Chamamos de menor complementar relativo a um elemento aij de uma matriz M, quadrada e de ordem n>1, o determinante MCij , de ordem n - 1, associado à matriz obtida de M quando suprimimos a linha e a coluna que passam por aij .
Vejamos como determiná-lo pelos exemplos a seguir:
a) Dada a matriz  , de ordem 2, para determinar o menor complementar relativo ao elemento a11(MC11), retiramos a linha 1 e a coluna 1:
, de ordem 2, para determinar o menor complementar relativo ao elemento a11(MC11), retiramos a linha 1 e a coluna 1:
 , de ordem 2, para determinar o menor complementar relativo ao elemento a11(MC11), retiramos a linha 1 e a coluna 1:
, de ordem 2, para determinar o menor complementar relativo ao elemento a11(MC11), retiramos a linha 1 e a coluna 1: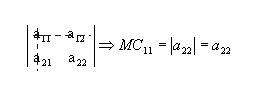
Da mesma forma, o menor complementar relativo ao elemento a12 é:
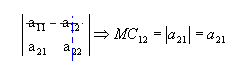
b) Sendo  , de ordem 3, temos:
, de ordem 3, temos:
 , de ordem 3, temos:
, de ordem 3, temos:segunda-feira, 15 de junho de 2015
MATRIZ
Boa Tarde
Conforme combinado segue vídeo sobre MATRIZ para estudarem para avaliação.
Boa Prova....
sexta-feira, 12 de junho de 2015
EXERCÍCIOS
Resolva as equações abaixo:
a) 5x2 - 3x - 2 = 0
b) 3x2 + 55 = 0
c) x2 - 6x = 0
d) x2 - 10x + 25 = 0
e) x2 - x - 20 = 0
f) x2 - 3x -4 = 0
g) x2 - 8x + 7 = 0
Assinar:
Comentários (Atom)