ANÁLISE COMBINATÓRIA

Alunos do 2º A e 2º C...segue o vídeo conforme combinado...

VÍDEOS SOBRE DETERMINANTE

VÍDEOS SOBRE DETERMINANTE

REGRA DE CRAMER

REGRA DE CRAMER

A regra de Cramer é uma das maneiras de resolver um sistema linear, mas só poderá ser utilizada na resolução de sistemas que o número de equações e o número de incógnitas forem iguais.

Portanto, ao resolvermos um sistema linear de n equações e n incógnitas para a sua resolução devemos calcular o determinante (D) da equação incompleta do sistema e depois substituirmos os termos independentes em cada coluna e calcular os seus respectivos determinantes e assim aplicar a regra de Cramer que diz:

Os valores das incógnitas são calculados da seguinte forma:

x₁ = D1
         D

x₂ = D2 
         D

x₃ = D3   ...   x_n = Dn
         D                    D

Veja no exemplo abaixo de como aplicar essa regra de Cramer:

Dado o sistema linear , para resolvê-lo podemos utilizar da regra de Cramer, pois ele possui 3 equações e 3 incógnitas, ou seja, o número de incógnitas é igual ao número de equações.

Devemos encontrar a matriz incompleta desse sistema linear que será chamada de A.


Agora calculamos o seu determinante que será representado por D.



D = 1 + 6 + 2 + 3 – 1 + 4
D = 15.

Agora devemos substituir os temos independentes na primeira coluna da matriz A, formando assim uma segunda matriz que será representada por Ax.



Agora calcularmos o seu determinante representado por Dx.



Dx = 8 + 4 + 3 + 2 – 8 + 6
Dx = 15

Substituímos os termos independentes na segunda coluna da matriz incompleta formando a matriz Ay.


Agora calcularmos o seu determinante Dy.



Dy = -3 + 24 + 4 – 9 – 2 + 16
Dy = 30

Substituindo os termos independentes do sistema na terceira coluna da matriz incompleta formaremos a matriz Az.


Agora calculamos o seu determinante representado por Dz.

Dz = – 2 + 18 + 16 + 24 – 3 – 8
Dz = 45

Depois de ter substituído todas as colunas da matriz incompleta pelos termos independentes, iremos colocar em prática a regra de Cramer.

A incógnita x = Dx = 15 = 1
                        D      15

A incógnita y = Dy = 30 = 2
                        D      15

A incógnita z = Dz = 45 = 3
                        D      15

Portanto, o conjunto verdade desse sistema será V = {(1,2,3)}.

Bom final de semana...

Prof Mauro Ricardo

Determinantes

Determinantes

   Como já vimos, matriz quadrada é a que tem o mesmo número de linhas e de colunas (ou seja, é do tipo nxn).

   A toda matriz quadrada está associado um número ao qual damos o nome de determinante.

   Dentre as várias aplicações dos determinantes na Matemática, temos:

• resolução de alguns tipos de sistemas de equações lineares;
• cálculo da área de um triângulo situado no plano cartesiano, quando são conhecidas as coordenadas dos seus vértices;

Determinante de 1ª ordem

   Dada uma matriz quadrada de 1ª ordem M=[a₁₁], o seu determinante é o número real a₁₁:

det M =Ia₁₁I = a₁₁

Observação: Representamos o determinante de uma matriz entre duas barras verticais, que não têm o significado de módulo.

   Por exemplo:

M= [5] det M = 5 ou I 5 I = 5

M = [-3] det M = -3 ou I -3 I = -3

Determinante de 2ª ordem

   Dada a matriz , de ordem 2, por definição o determinante associado a M, determinante de 2ª ordem, é dado por: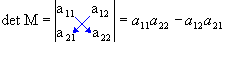

    Portanto, o determinante de uma matriz de ordem 2 é dado pela diferença entre o produto dos elementos da diagonal principal e o produto dos elementos da diagonal secundária. Veja o exemplo a seguir.

   

                        

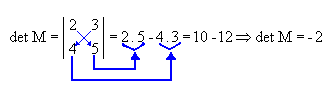
Menor complementar

   Chamamos de menor complementar relativo a um elemento a_ij de uma matriz M, quadrada e de ordem n>1, o determinante MC_ij , de ordem n - 1, associado à matriz obtida de M quando suprimimos a linha e a coluna que passam por a_ij .

   Vejamos como determiná-lo pelos exemplos a seguir:

a) Dada a matriz , de ordem 2, para determinar o menor complementar relativo ao elemento a₁₁(MC₁₁), retiramos a linha 1 e a coluna 1: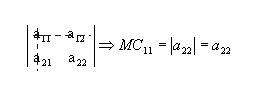

Da mesma forma, o menor complementar relativo ao elemento a₁₂ é:

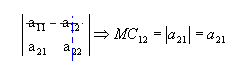
b) Sendo , de ordem 3, temos:

Atenção, 

Conforme combinado segue material sobre DETERMINANTE.

Bons estudos....

MATRIZ

Boa Tarde 

Conforme combinado segue vídeo sobre MATRIZ para estudarem para avaliação.

Boa Prova....

EXERCÍCIOS

Resolva as equações abaixo:

a) 5x² - 3x - 2 = 0

b) 3x²  + 55 = 0

c) x² - 6x = 0

d) x² - 10x + 25 = 0

e) x² - x - 20 = 0

f) x² - 3x -4 = 0

g) x² - 8x + 7 = 0

DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS

DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS

Números amigos

Pitágoras considerava que alguns números eram amigos de outros números ... Ele costumava relacionar todos os divisores de um número e depois somá-los. Por exemplo, os divisores do número 10 são 1, 2 e 5, com soma 1 + 2 + 5 = 8. Números amigos são aqueles cujos divisores somados se reproduzem reciprocamente, como 220 e 284. Os divisores de 220 são 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 e 110, cuja soma é 284. Por sua vez, 284 tem como divisores 1, 2, 4, 71 e 142, cuja soma é 220. Por isso 220 e 284 são números amigos ou amigáveis. 

Além de Pitágoras, outros matemáticos importantes gostavam de estudar os números amigos, como Pierre de Fermat e Leonardo Euler. Fermat descobriu os números amigos 17.296 e 18.416, e Euler, certa vez, publicou uma lista de trinta pares de números amigos, ele que mais tarde iria enriquecer essa lista com mais três dezenas desses pares.Todos os pares de números amigos inferiores a um milhão já são conhecidos.

O conceito de números amigos é extensivamente utilizado nas práticas de feitiçaria, magia e astrologia e na confecção de horóscopos.

DEMONSTRAÇÃO DE PITÁGORAS

DEMONSTRAÇÃO DE PITÁGORAS

Bom dia 

Caros alunos,


Lute com determinação, 

abrace a vida com paixão, 

perca com classe e vença com ousadia, 

porque o mundo pertence a quem se atreve 

e a vida é muito para ser insignificante.

#bom dia 

Prof Mauro Ricardo

VÍDEO TRAPÉZIO

Segue mais um vídeo interessante....

TRAPÉZIO

Há certa discordância em relação a quantos lados paralelos são permitidos em um trapézio. O que está em questão é se os paralelogramos, que possuem dois pares de lados paralelos, devem ser considerados trapézios. Alguns autores definem um trapézio como sendo um quadrilátero que possui exatamente um par de lados paralelos, excluindo portanto os paralelogramos. Outros autores definem um trapézio como um quadrilátero em que há pelo menos um par de lados paralelos, de modo que neste caso o paralelogramo é um tipo especial de trapézio (juntamente com o losango, o retângulo e o quadrado). Essa última definição é consistente com o uso feito em matemática superior, por exemplo no cálculo. A primeira definição faria com que conceitos tais como o da aproximação trapezoidal para a integral definida fossem mal definidos.

A área A de um trapézio simples (isto é, sem auto-interseções) é dada por: 

em que B e b são os comprimentos dos lados paralelos (as base maior e menor) e h é a altura (a distância entre esses lados). Em 499 EC Aryabhata, um grande matemático-astrônomo da era clássica da matemática e física indiana, usou este método no Ariabatiia. A fórmula anterior tem como caso particular a fórmula que fornece a área de um triângulo, considerando-se um triângulo como um trapézio degenerado em que um dos lados paralelos foi reduzido a um único ponto.

A mediana do trapézio é o segmento que une os pontos médios dos lados não paralelos. O seu comprimento m é igual à média dos comprimentos das bases do trapézio:

Consequentemente, a área do trapézio é calculada pela multiplicação de sua mediana por sua altura:

O lado de um trapézio retângulo pode ser calculado pela formula:

 Relação de Euler

RELAÇÃO DE EULER

A relação criada pelo matemático suíço Leonhard Euler possui extrema importância na determinação do número de arestas, vértices e faces de qualquer poliedro convexo e alguns não convexos. Essa relação permite que os cálculos sejam realizados no intuito de determinarmos o número de elementos de um poliedro. A fórmula criada por Euler é a seguinte: 

V – A + F = 2, onde V = número de vértices, A = número de arestas e F = número de faces. 


Exemplo 1 

Determine o número de faces de um sólido que possui 10 arestas e 6 vértices. 
Resolução: 
V – A + F = 2 
6 – 10 + F = 2 
–4 + F = 2 
F = 4 + 2 
F = 6 
Portanto, o sólido possui 6 faces. 

Exemplo 2 

Determine o número de vértices da pirâmide quadrangular a seguir:

Visivelmente podemos afirmar que a pirâmide possui 5 vértices, 5 faces e 8 arestas. Vamos agora demonstrar que a relação de Euler é válida na determinação dos elementos da pirâmide de base quadrangular. 
Resolução: 
Vértices 
V – A + F = 2 
V – 8 + 5 = 2 
V = 2 + 3 
V = 5 

Arestas 
V – A + F = 2 
5 – A + 5 = 2 
–A = 2 – 10 
–A = –8 x(–1) 
A = 8 

Faces 
V – A + F = 2 
5 – 8 + F = 2 
–3 + F = 2 
F = 2 + 3 
F = 5 

Podemos notar que a relação de Euler é realmente válida na determinação dos elementos de um sólido convexo. 

Exemplo 3 

O número de faces de um poliedro convexo de 22 arestas é igual ao número de vértices. Determine, utilizando a relação de Euler, o número de faces do poliedro. 
Resolução: 
Considerando que o número de faces é igual ao número de vértices, podemos representar os valores desconhecidos pela incógnita x. Dessa forma, F = x e V = x. 

Aplicando a relação de Euler: 
V – A + F = 2 
x – 22 + x = 2 
2x = 2 + 22 
2x = 24 
x = 12 

Portanto, o número de faces do poliedro com 22 arestas é igual a12.

Boa noite

Alunos,

Em breve postarei a resolução da Olimpíada de Matemática.

Espero que tenham obtido êxito....

Aguardem....

abs

Prof. Mauro Ricardo

EXERCÍCIO RESOLVIDO SOBRE ESFERA

1) (UFPR) Duas esferas metálicas maciças, uma com raio igual a 4 cm e a outra com raio de 8 cm, são fundidas e moldadas em forma de um cilindro circular reto com altura igual a 12 cm. Determine, em cm, o raio do cilindro.

Resolução:

Esferas são bolas maciças com um eixo central, uma linha que passa pelo centro dividindo a esfera e um ponto central, o centro da esfera, de onde qualquer segmento que dali parta até a extremidade será o raio.Para calcular a área, que é a casca da esfera temos:
A = 4πR²

Para o volume:
V = 4πR³
       3
Ou seja, tendo o raio, você tem tudo na esfera.

Na questão vamos determinar o volume das esferas que será o volume do cilindro:
Esfera 1
V = 4πR³
       3
V = 4π4³
       3
V = 4π64
       3
V = 256π
         3

Esfera 2
V = 4π8³
       3
V = 4π512
       3
V = 2048π
          3
Somando os volumes:
256π+2048π
   3         3
2304π
   3
768π

Como foram transformadas em um cilindro, temos o volume e a altura, encontramos o raio:
Vcilindro = πR².h
768π = πR².12
768 = 12R²
R²=64
R=8

_________________________________________________________________________

EXERCÍCIO RESOLVIDO SOBRE ESFERA

 (ENEM-2010) Se pudéssemos reunir em esferas toda a água do planeta, os diâmetros delas seriam:

A razão entre o volume da esfera que corresponde à água doce superficial e o volume da esfera que corresponde à água doce do planeta é

a) 1/343 

b) 1/49 

c) 1/7 

d) 29/136 

e) 136/203 

RESOLUÇÃO: 

Vamos considerar V1 e V2 o volume da esfera que corresponde à água doce superficial e o volume da esfera que corresponde à água doce do planeta, respectivamente.

Portanto, Gabarito é letra A.